Publication bias is real. In the social sciences, more than one study finds that statistically significant results seem to be about three times more likely to be published than insignificant ones. Some estimates from medicine aren’t so bad, but a persistent bias in favor of positive results remains. What about science more generally?
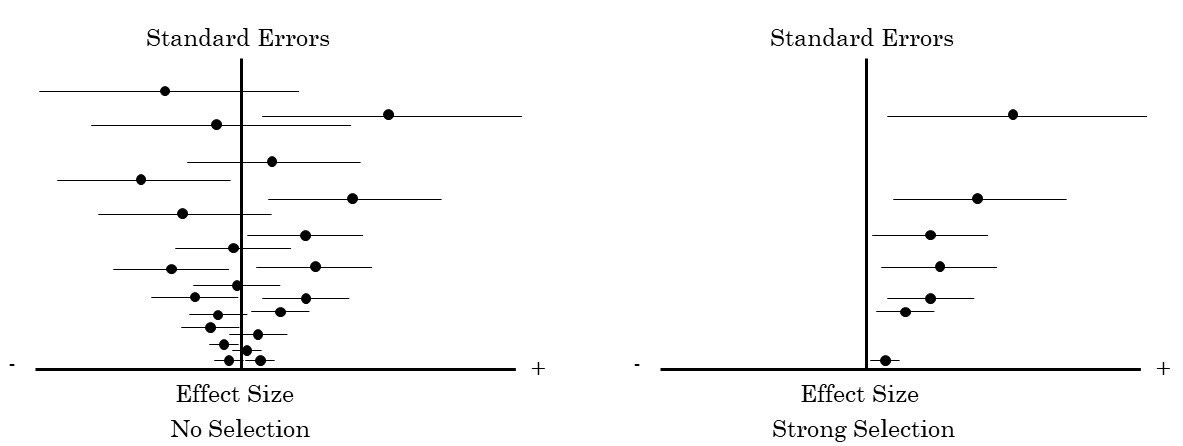
To answer that question, you need a way to measure bias across fields that might be very different in terms of their methodology. One way is to look for a correlation between the size of the standard error and the estimated size of an effect. In the absence of publication bias, there shouldn’t be a relationship between these two things. To see why, suppose your study has a lot of data points. In that case, you should be able to get a very precise estimate that is close to the actual population average of the thing you’re studying. On the other hand, if your study has very few data points, you’ll get a very imprecise estimate, including a high probability of getting something very much bigger than the actual population mean and a high probability of getting something very much smaller. But over lots of studies, if there’s no publication bias, you’ll get some abnormally high estimates, some abnormally low ones, but in the end they’ll cancel each other out. If, however, small estimates are systematically excluded from publication, then you’ll end up with a robust correlation between the size of your standard errors and the size of your effects. The extent of this correlation is a way to measure the extent of publication bias in a given literature.
(A downside of this approach is that it will only work in disciplines where this framework makes sense; where research is primarily about measuring effect sizes with noisy data. But enough disciplines do this that it’s a start.)
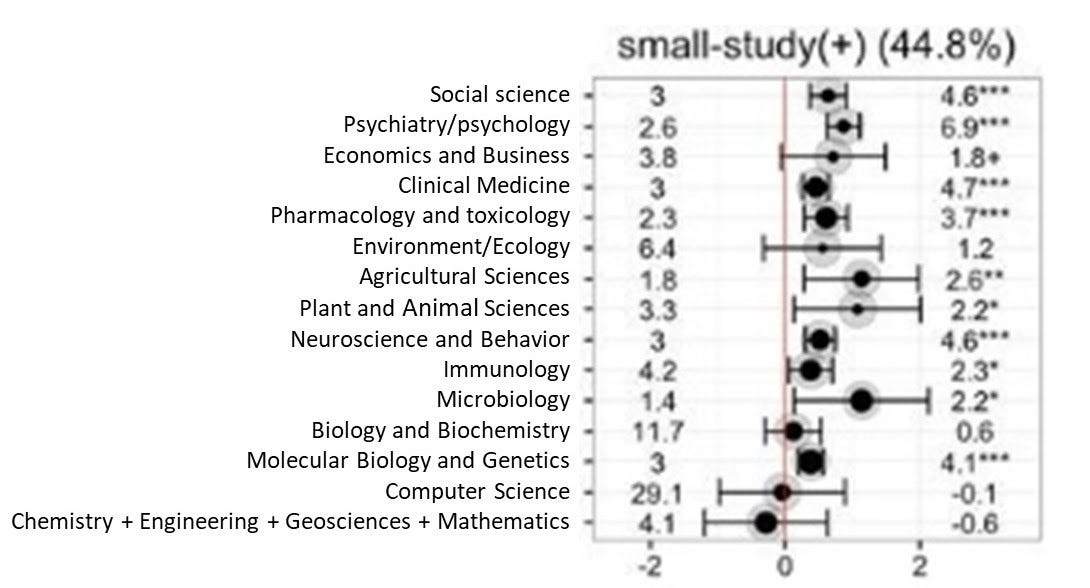
Fanelli, Costas, and Ioannidis (2017) obtain 1,910 meta-analyses drawn from all areas of science, and pull from these 33,355 datapoints from original underlying studies. For each meta-analysis, they compute the correlation between the standard error and the size of the estimated effect; they then do a weighted average across the different meta-analyses to generate a sort of average over the meta-analyses in fields they cover. In general, the more positive the estimate, the stronger the correlation between standard errors and effect size, implying stronger publication bias. Results below:
Note that the social sciences (up at the top) have pretty high measures of bias, estimated with a lot of precision, while many (but not all) of the biological fields also have fairly high bias. But also note the bottom two rows, which seem to exhibit no bias: computer science, chemistry, engineering, geosciences, and mathematics.
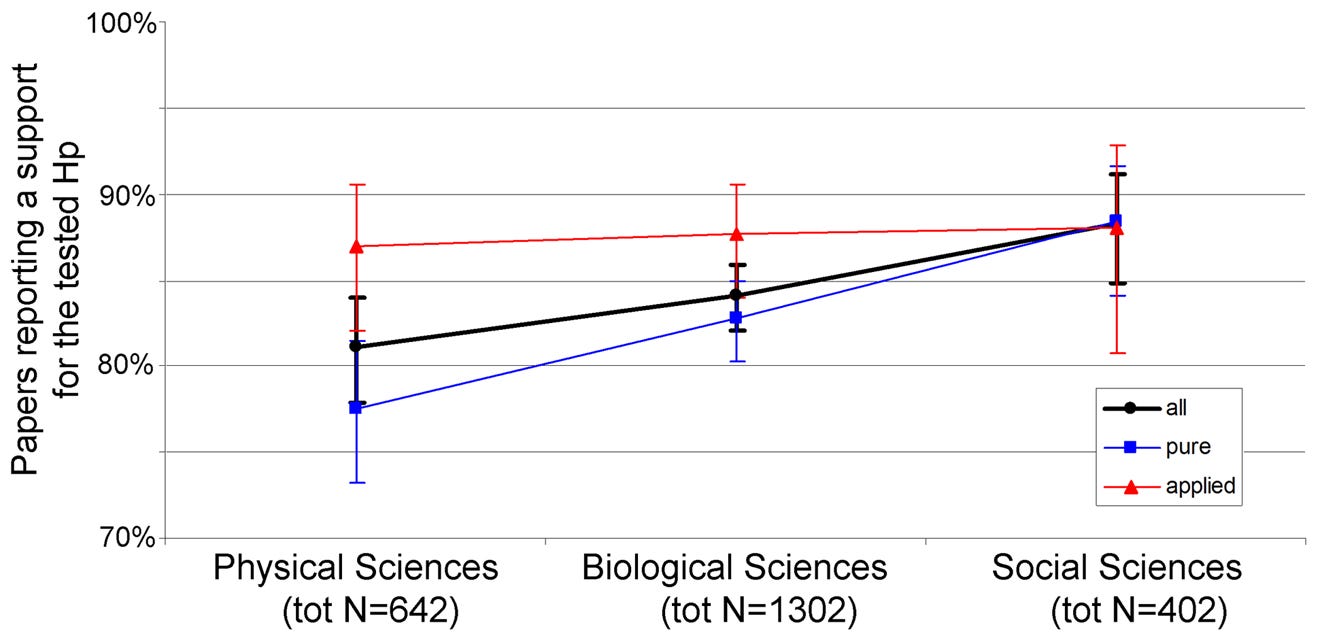
As noted already though, this method of measuring bias might not be appropriate for all fields, since it is rigidly defined in terms of sampling from noisy data. Fanelli (2010) uses a simpler, but more flexible measure of publication bias. Fanelli analyses a random sample of 2,434 papers from all disciplines that include some variation of the phrase “test the hypothesis.” For each paper, Fanelli determined if the authors of the paper argued they had found positive evidence for their hypothesis or not (that is, they either found no evidence in favor of the hypothesis, or actually found contrary results). As a rough and ready test of publication bias, he then looked at the share of hypotheses in each field for which positive support was found. He finds between 75 and 90% of hypotheses mentioned in published papters tend to be supported, across different disciplines. But there are some significant differences across disciplines.
Fanelli cuts papers into six categories: physical sciences, biological sciences, and social sciences, and for each one he further sub-divides papers into pure science and applied science. There are no major differences among applied papers in all three domains - bias seems to be quite high in every case. But in the pure science fields, physical sciences tended to find support for less than 80% of their hypotheses while social sciences tended to find support for nearly 90% of the hypotheses investigated. Biology is in the middle.
Taken together, these two studies suggest the social sciences have bigger problems with publication bias than do the biological sciences, which tend to have more problems than the hard sciences. Why?
What Drives Bias Across Fields?
Let me run through three possible explanations, before looking at one of the few studies that can provide evidence. Note that there are probably more possible explanations, and they’re not mutually exclusive. As far as I can tell, there is very little work on this question (please email me if you know of other relevant work - I would love to hear about it).
First, variation in publication bias could be related to the nature of publication in different fields. If it’s easier to draft and push an article through peer review in some fields than in others then some fields may end up getting more results out there (even if they’re not out there in a top-ranked journal). In the social sciences, we have some evidence that the biggest difference between null results and strong results is that most null results are never even written up and submitted for publication. Maybe that’s because it’s too much work for too little reward. In a field where writing up and publishing results from an experiment somewhere is easy, it might be worth doing, if only to add another line to the CV.
Second, variation in publication bias could be related to the nature of data in different fields. It may be easier in some fields to tightly control for noise in data, or to obtain many more observations, than in others. In economics, a big sample might be hundreds of thousands of observations. In physics, the Large Hadron Collider generates 30 petabytes of data per year. In fields where clean data is plentiful, it might not be the case that when you run an experiment sometimes you find support for a hypothesis and sometimes you don’t. You always find the same thing, or at least always come to the same conclusion about statistical significance. In that case, you won’t find much of a relationship between the size of standard errors and effect sizes: within the range of observed standard errors, everything is either significant or not.
Lastly, it may be that fields differ in their criteria for deciding what is worth publishing. The root cause of publication bias is that journals want to highlight notable research, in order to be relevant to their readership. But what counts as notable research?
Suppose that empirical research is most notable when it provides support for specific theories. In that case, a question in which multiple competing theories make different predictions might exhibit less publication bias. If there is a theory that predicts a null result, and another theory that predicts a statistically significant result, and we don’t have good evidence on which theory is correct, then either result is notable and helps us understand how the world works. Consequently, a journal should be more willing to publish either result.
It might be the case, for example, that the hard sciences have sufficiently established theories such that null results are quite surprising when they are found, and hence easier to publish. In the social sciences, in contrast, we’re just not there yet. Instead, we have an unstated assumption that most hypotheses are false. When we fail to find evidence for one of these hypotheses, it’s not surprising or notable, and so harder to publish.
A bit of evidence from economics
To shed a little light on these questions, let’s look at one more study of differential bias. We’ve seen some evidence that bias varies across major disciplines. But we also have some evidence that bias varies within a particular discipline.
Doucouliagos and Stanley (2013) looks at 87 different meta-analyses from empirical economics and measure the extent of publication bias in each of the literatures covered using the approach already covered, where standard errors are compared with effect sizes. In the figure below, they classify anything smaller than 1 as exhibiting little to modest selection bias, anything between 1 and 2 as exhibiting substantial selection bias, and anything over 2 as exhibiting severe selection bias. They find there are plenty of results in each category.
What drives different levels of bias in economics?
I think it is less likely that variation in publication bias within economics is driven by different publication standards within the different meta-analyses covered. In many cases, these literature are publishing in the exact same journals, but on different questions.
Doucouliagos and Stanley provide a bit more evidence that publication bias might be related to data though. My subjective read on the quality of data across economic fields is that macroeconomics has the toughest time with getting lots of clean data. And Doucouliagos and Stanley do find publication bias seems to more extreme in macroeconomics than other fields.
But Doucouliagos and Stanley (2013) is really set up to test the third explanation: that differences in the range of values permitted by theory explain a big chunk of the variation in publication bias across fields. How are you going to measure that though?
Doucouliagos and Stanley take a few different approaches. First, they just use their own judgement to code up each meta-analysis as pertaining to a question where theory predicts empirical results can go either way (i.e., positive or negative). Second, they use their own reading of the meta-analyses or draw on surveys (where they exist) to assess whether there is “considerable” debate around this area of research. Whereas they claim their first measure is non-controversial and that most economists would agree with how they code things, they acknowledge the second criteria is a subjective one.
By both of these measures, they find that when theory admits a wider array of results, there is less evidence of publication bias. And the effects are pretty large. A field whose theory they code as admitting positive and negative results has a lot less bias than one that doesn’t - the difference is large enough to drop from “severe” selection bias to “little or no” selection bias, for example.
But maybe we’re worried at this point that we have the direction of causality exactly backwards. Maybe it’s not that wider theory permits a wider array of results to be published. Maybe it’s that a wider array of published results leads theorists to come up with wider theories to accommodate this evidence. Doucouliagos and Stanley have two responses here. First, there is a difference between the breadth of results published and publication bias and they try to control for the former to really isolate the latter. After all, it is possible for a field to have both selection bias and a wide breadth of results published. Their methodology can separately identify both, at least in theory, and so they can check if there is more selection bias when there is more accommodating theory, even when two fields have an otherwise similarly large array of results to explain.
But in practice, I wonder if controlling for this is hard to do. So I am a fan of the second approach they take to address this issue. There are some theories in economics where there just really isn’t much wiggle room about which way the results are supposed to go. One of them is studies estimating demand. Except for some exotic cases, economists expect that if you hold all else constant, when prices go up, demand should go down, and vice-versa. We even permit ourselves to call this the “law” of demand. Economists almost uniformly will believe that apparent violations of this can be explained by a failure to control for confounding factors. They will strongly resist the temptation to derive new theories that predict demand and price go up or down together.
Moreover, it isn’t controversial to identify which meta-analyses are about estimating demand and which are not. So for their final measure, Doucouliagos and Stanley look at estimates of bias in studies that estimate demand and those that don’t. And they find studies that estimate demand exhibit much more selection bias than those that don’t (even more than in their measures about extent of debate or what theory permits). In other words, when economists get results that say there is no relationship between price and demand, or that demand goes up when prices go up, these results appear less likely to be published.
So, at least in this context, if your theory admits a wider array of “notable” findings, then you seem to have less trouble getting findings published. Of course, this is just one study, so I want to be cautious leaning too heavily on it. Indeed - who knows if others have looked for the same relationships elsewhere and gotten different results, but have been unable to publish them? (Joking! Mostly.)
If you liked this post, you might also like:









Share this post